\( \DeclareMathOperator{\abs}{abs} \newcommand{\ensuremath}[1]{\mbox{$#1$}} \)

The double pendulum in Maxima

José A Vallejo
Faculty of Sciences
State University of San Luis Potosí (México)
URL: http://galia.fc.uaslp.mx/~jvallejo
Email: jvallejo@fc.uaslp.mx

ABSTRACT: This wxMaxima worksheet is just an adaptation of the really amazing Physics Lab
presented in https://www.myphysicslab.com/pendulum/double-pendulum-en.html (which is
done in Javascript). Go there for details of the dynamics and to see a wonderful interactive
applet.

1 Theoretical preliminaries

First, we consider the equations resulting from the balance of forces. For the upper pendulum
we have:

(%i1) eq1:m[1]·a[x,1]=−T[1]·sin(%theta[1])+T[2]·sin(%theta[2]);
\[\tag{eq1}{m_1}\, {a_{x,1}}={T_2} \sin{\left( {{\theta }_2}\right) }-{T_1} \sin{\left( {{\theta }_1}\right) }\]
(%i2) eq2:m[1]·a[y,1]=T[1]·cos(%theta[1])−T[2]·cos(%theta[2])−m[1]·g;
\[\tag{eq2}{m_1}\, {a_{y,1}}=-{m_1} g-{T_2} \cos{\left( {{\theta }_2}\right) }+{T_1} \cos{\left( {{\theta }_1}\right) }\]

For the lower pendulum:

(%i3) eq3:m[2]·a[x,2]=−T[2]·sin(%theta[2]);
\[\tag{eq3}{m_2}\, {a_{x,2}}=-{T_2} \sin{\left( {{\theta }_2}\right) }\]
(%i4) eq4:m[2]·a[y,2]=T[2]·cos(%theta[2])−m[2]·g;
\[\tag{eq4}{m_2}\, {a_{y,2}}={T_2} \cos{\left( {{\theta }_2}\right) }-{m_2} g\]

In https://www.myphysicslab.com/pendulum/double-pendulum-en.html, the first step to
get the equations of motion is

(%i5) eq5:eq1+eq3;
\[\tag{eq5}{m_2}\, {a_{x,2}}+{m_1}\, {a_{x,1}}=-{T_1} \sin{\left( {{\theta }_1}\right) }\]
(%i6) eq6:eq2+eq4;
\[\tag{eq6}{m_2}\, {a_{y,2}}+{m_1}\, {a_{y,1}}=-{m_2} g-{m_1} g+{T_1} \cos{\left( {{\theta }_1}\right) }\]

The second step consists in

(%i7) eq7:cos(%theta[1])·eq5;
\[\tag{eq7}\cos{\left( {{\theta }_1}\right) } \left( {m_2}\, {a_{x,2}}+{m_1}\, {a_{x,1}}\right) =-{T_1} \cos{\left( {{\theta }_1}\right) } \sin{\left( {{\theta }_1}\right) }\]
(%i8) eq8:sin(%theta[1])·eq6;
\[\tag{eq8}\sin{\left( {{\theta }_1}\right) } \left( {m_2}\, {a_{y,2}}+{m_1}\, {a_{y,1}}\right) =\sin{\left( {{\theta }_1}\right) } \left( -{m_2} g-{m_1} g+{T_1} \cos{\left( {{\theta }_1}\right) }\right) \]

From these, we get (in the third step):

(%i9) eq7+eq8;
\[\tag{%o9} \sin{\left( {{\theta }_1}\right) } \left( {m_2}\, {a_{y,2}}+{m_1}\, {a_{y,1}}\right) +\cos{\left( {{\theta }_1}\right) } \left( {m_2}\, {a_{x,2}}+{m_1}\, {a_{x,1}}\right) =\sin{\left( {{\theta }_1}\right) } \left( -{m_2} g-{m_1} g+{T_1} \cos{\left( {{\theta }_1}\right) }\right) -{T_1} \cos{\left( {{\theta }_1}\right) } \sin{\left( {{\theta }_1}\right) }\]

or

(%i10) eq9:ratsimp(%);
\[\tag{eq9}{m_2} \sin{\left( {{\theta }_1}\right) } {a_{y,2}}+{m_1} \sin{\left( {{\theta }_1}\right) } {a_{y,1}}+{m_2} \cos{\left( {{\theta }_1}\right) } {a_{x,2}}+{m_1} \cos{\left( {{\theta }_1}\right) } {a_{x,1}}=\left( -{m_2}-{m_1}\right) \sin{\left( {{\theta }_1}\right) } g\]

Now we do something similar with the lower pendulum, but just in one shot:

(%i11) cos(%theta[2])·eq3+sin(%theta[2])·eq4;
\[\tag{%o11} {m_2} \sin{\left( {{\theta }_2}\right) } {a_{y,2}}+{m_2} \cos{\left( {{\theta }_2}\right) } {a_{x,2}}=\sin{\left( {{\theta }_2}\right) } \left( {T_2} \cos{\left( {{\theta }_2}\right) }-{m_2} g\right) -{T_2} \cos{\left( {{\theta }_2}\right) } \sin{\left( {{\theta }_2}\right) }\]
(%i12) eq10:ratsimp(%);
\[\tag{eq10}{m_2} \sin{\left( {{\theta }_2}\right) } {a_{y,2}}+{m_2} \cos{\left( {{\theta }_2}\right) } {a_{x,2}}=-{m_2} \sin{\left( {{\theta }_2}\right) } g\]

In https://www.myphysicslab.com/pendulum/double-pendulum-en.html it is stated that
these are equations for %alpha[1], %alpha[2], the second derivatives of %theta[1], %theta[2],
respectively. This is so because we have some orther relations (in which we are using
the notation %omega[1], %omega[2] for the first derivatives of %theta[1], %theta[2] with
respect to time):

(%i13) a[x,1]:−(%omega[1])^2·L1·sin(%theta[1])+%alpha[1]·L1·cos(%theta[1]);
\[\tag{%o13} {{\alpha }_1} \cos{\left( {{\theta }_1}\right) } \mathit{L1}-{{\omega }_{1}^{2}} \sin{\left( {{\theta }_1}\right) } \mathit{L1}\]
(%i14) a[y,1]:(%omega[1])^2·L1·cos(%theta[1])+%alpha[1]·L1·sin(%theta[1]);
\[\tag{%o14} {{\alpha }_1} \sin{\left( {{\theta }_1}\right) } \mathit{L1}+{{\omega }_{1}^{2}} \cos{\left( {{\theta }_1}\right) } \mathit{L1}\]
(%i15) a[x,2]:a[x,1]−(%omega[2])^2·L2·sin(%theta[2])+%alpha[2]·L2·cos(%theta[2]);
\[\tag{%o15} -{{\omega }_{2}^{2}} \sin{\left( {{\theta }_2}\right) } \mathit{L2}+{{\alpha }_2} \cos{\left( {{\theta }_2}\right) } \mathit{L2}-{{\omega }_{1}^{2}} \sin{\left( {{\theta }_1}\right) } \mathit{L1}+{{\alpha }_1} \cos{\left( {{\theta }_1}\right) } \mathit{L1}\]
(%i16) a[y,2]:a[y,1]+(%omega[2])^2·L2·cos(%theta[2])+%alpha[2]·L2·sin(%theta[2]);
\[\tag{%o16} {{\alpha }_2} \sin{\left( {{\theta }_2}\right) } \mathit{L2}+{{\omega }_{2}^{2}} \cos{\left( {{\theta }_2}\right) } \mathit{L2}+{{\alpha }_1} \sin{\left( {{\theta }_1}\right) } \mathit{L1}+{{\omega }_{1}^{2}} \cos{\left( {{\theta }_1}\right) } \mathit{L1}\]

Taking this into account, equations eq9 and eq10 become (notice the use of '' to evaluate
a[i,j])

(%i17) eq11:''eq9;
\[\tag{eq11}{m_2} \cos{\left( {{\theta }_1}\right) } \left( -{{\omega }_{2}^{2}} \sin{\left( {{\theta }_2}\right) } \mathit{L2}+{{\alpha }_2} \cos{\left( {{\theta }_2}\right) } \mathit{L2}-{{\omega }_{1}^{2}} \sin{\left( {{\theta }_1}\right) } \mathit{L1}+{{\alpha }_1} \cos{\left( {{\theta }_1}\right) } \mathit{L1}\right) +{m_2} \sin{\left( {{\theta }_1}\right) } \left( {{\alpha }_2} \sin{\left( {{\theta }_2}\right) } \mathit{L2}+{{\omega }_{2}^{2}} \cos{\left( {{\theta }_2}\right) } \mathit{L2}+{{\alpha }_1} \sin{\left( {{\theta }_1}\right) } \mathit{L1}+{{\omega }_{1}^{2}} \cos{\left( {{\theta }_1}\right) } \mathit{L1}\right) +{m_1} \cos{\left( {{\theta }_1}\right) } \left( {{\alpha }_1} \cos{\left( {{\theta }_1}\right) } \mathit{L1}-{{\omega }_{1}^{2}} \sin{\left( {{\theta }_1}\right) } \mathit{L1}\right) +{m_1} \sin{\left( {{\theta }_1}\right) } \left( {{\alpha }_1} \sin{\left( {{\theta }_1}\right) } \mathit{L1}+{{\omega }_{1}^{2}} \cos{\left( {{\theta }_1}\right) } \mathit{L1}\right) =\left( -{m_2}-{m_1}\right) \sin{\left( {{\theta }_1}\right) } g\]
(%i18) eq12:''eq10;
\[\tag{eq12}{m_2} \cos{\left( {{\theta }_2}\right) } \left( -{{\omega }_{2}^{2}} \sin{\left( {{\theta }_2}\right) } \mathit{L2}+{{\alpha }_2} \cos{\left( {{\theta }_2}\right) } \mathit{L2}-{{\omega }_{1}^{2}} \sin{\left( {{\theta }_1}\right) } \mathit{L1}+{{\alpha }_1} \cos{\left( {{\theta }_1}\right) } \mathit{L1}\right) +{m_2} \sin{\left( {{\theta }_2}\right) } \left( {{\alpha }_2} \sin{\left( {{\theta }_2}\right) } \mathit{L2}+{{\omega }_{2}^{2}} \cos{\left( {{\theta }_2}\right) } \mathit{L2}+{{\alpha }_1} \sin{\left( {{\theta }_1}\right) } \mathit{L1}+{{\omega }_{1}^{2}} \cos{\left( {{\theta }_1}\right) } \mathit{L1}\right) =-{m_2} \sin{\left( {{\theta }_2}\right) } g\]

Now, we want to solve for the angular accelerations %alpha[1] and %alpha[2]. This is easy for
Maxima (or any other CAS), because the equations are linear with respect to those variables:

(%i19) solve([eq11,eq12],[%alpha[1],%alpha[2]]);
\[\tag{%o19} [[{{\alpha }_1}=-(\left( {m_1} \sin{\left( {{\theta }_1}\right) } {{\sin{\left( {{\theta }_2}\right) }}^{2}}-{m_2} \cos{\left( {{\theta }_1}\right) } \cos{\left( {{\theta }_2}\right) } \sin{\left( {{\theta }_2}\right) }+\left( {m_2}+{m_1}\right) \sin{\left( {{\theta }_1}\right) } {{\cos{\left( {{\theta }_2}\right) }}^{2}}\right) g+\left( -{{\omega }_{2}^{2}}\, {m_2} \cos{\left( {{\theta }_1}\right) } {{\sin{\left( {{\theta }_2}\right) }}^{3}}+{{\omega }_{2}^{2}}\, {m_2} \sin{\left( {{\theta }_1}\right) } \cos{\left( {{\theta }_2}\right) } {{\sin{\left( {{\theta }_2}\right) }}^{2}}-{{\omega }_{2}^{2}}\, {m_2} \cos{\left( {{\theta }_1}\right) } {{\cos{\left( {{\theta }_2}\right) }}^{2}} \sin{\left( {{\theta }_2}\right) }+{{\omega }_{2}^{2}}\, {m_2} \sin{\left( {{\theta }_1}\right) } {{\cos{\left( {{\theta }_2}\right) }}^{3}}\right) \, \mathit{L2}+\left( -{{\omega }_{1}^{2}}\, {m_2} \cos{\left( {{\theta }_1}\right) } \sin{\left( {{\theta }_1}\right) } {{\sin{\left( {{\theta }_2}\right) }}^{2}}+\left( {{\omega }_{1}^{2}}\, {m_2}\, {{\sin{\left( {{\theta }_1}\right) }}^{2}}-{{\omega }_{1}^{2}}\, {m_2}\, {{\cos{\left( {{\theta }_1}\right) }}^{2}}\right) \cos{\left( {{\theta }_2}\right) } \sin{\left( {{\theta }_2}\right) }+{{\omega }_{1}^{2}}\, {m_2} \cos{\left( {{\theta }_1}\right) } \sin{\left( {{\theta }_1}\right) } {{\cos{\left( {{\theta }_2}\right) }}^{2}}\right) \, \mathit{L1})/(\left( \left( {m_1}\, {{\sin{\left( {{\theta }_1}\right) }}^{2}}+\left( {m_2}+{m_1}\right) \, {{\cos{\left( {{\theta }_1}\right) }}^{2}}\right) \, {{\sin{\left( {{\theta }_2}\right) }}^{2}}-2 {m_2} \cos{\left( {{\theta }_1}\right) } \sin{\left( {{\theta }_1}\right) } \cos{\left( {{\theta }_2}\right) } \sin{\left( {{\theta }_2}\right) }+\left( \left( {m_2}+{m_1}\right) \, {{\sin{\left( {{\theta }_1}\right) }}^{2}}+{m_1}\, {{\cos{\left( {{\theta }_1}\right) }}^{2}}\right) \, {{\cos{\left( {{\theta }_2}\right) }}^{2}}\right) \, \mathit{L1}),{{\alpha }_2}=-(\left( \left( {m_2}+{m_1}\right) \, {{\cos{\left( {{\theta }_1}\right) }}^{2}} \sin{\left( {{\theta }_2}\right) }+\left( -{m_2}-{m_1}\right) \cos{\left( {{\theta }_1}\right) } \sin{\left( {{\theta }_1}\right) } \cos{\left( {{\theta }_2}\right) }\right) g+\left( {{\omega }_{2}^{2}}\, {m_2} \cos{\left( {{\theta }_1}\right) } \sin{\left( {{\theta }_1}\right) } {{\sin{\left( {{\theta }_2}\right) }}^{2}}+\left( {{\omega }_{2}^{2}}\, {m_2}\, {{\cos{\left( {{\theta }_1}\right) }}^{2}}-{{\omega }_{2}^{2}}\, {m_2}\, {{\sin{\left( {{\theta }_1}\right) }}^{2}}\right) \cos{\left( {{\theta }_2}\right) } \sin{\left( {{\theta }_2}\right) }-{{\omega }_{2}^{2}}\, {m_2} \cos{\left( {{\theta }_1}\right) } \sin{\left( {{\theta }_1}\right) } {{\cos{\left( {{\theta }_2}\right) }}^{2}}\right) \, \mathit{L2}+\left( \left( \left( {{\omega }_{1}^{2}}\, {m_2}+{{\omega }_{1}^{2}}\, {m_1}\right) \cos{\left( {{\theta }_1}\right) } {{\sin{\left( {{\theta }_1}\right) }}^{2}}+\left( {{\omega }_{1}^{2}}\, {m_2}+{{\omega }_{1}^{2}}\, {m_1}\right) \, {{\cos{\left( {{\theta }_1}\right) }}^{3}}\right) \sin{\left( {{\theta }_2}\right) }+\left( \left( -{{\omega }_{1}^{2}}\, {m_2}-{{\omega }_{1}^{2}}\, {m_1}\right) \, {{\sin{\left( {{\theta }_1}\right) }}^{3}}+\left( -{{\omega }_{1}^{2}}\, {m_2}-{{\omega }_{1}^{2}}\, {m_1}\right) \, {{\cos{\left( {{\theta }_1}\right) }}^{2}} \sin{\left( {{\theta }_1}\right) }\right) \cos{\left( {{\theta }_2}\right) }\right) \, \mathit{L1})/(\left( \left( {m_1}\, {{\sin{\left( {{\theta }_1}\right) }}^{2}}+\left( {m_2}+{m_1}\right) \, {{\cos{\left( {{\theta }_1}\right) }}^{2}}\right) \, {{\sin{\left( {{\theta }_2}\right) }}^{2}}-2 {m_2} \cos{\left( {{\theta }_1}\right) } \sin{\left( {{\theta }_1}\right) } \cos{\left( {{\theta }_2}\right) } \sin{\left( {{\theta }_2}\right) }+\left( \left( {m_2}+{m_1}\right) \, {{\sin{\left( {{\theta }_1}\right) }}^{2}}+{m_1}\, {{\cos{\left( {{\theta }_1}\right) }}^{2}}\right) \, {{\cos{\left( {{\theta }_2}\right) }}^{2}}\right) \, \mathit{L2})]]\]

Let us reorganize the output in a more manageable form:

(%i20) ratsimp(trigreduce(%));
\[\tag{%o20} [[{{\alpha }_1}=-\frac{\left( {m_2} \sin{\left( 2 {{\theta }_2}-{{\theta }_1}\right) }+\left( -{m_2}-2 {m_1}\right) \sin{\left( {{\theta }_1}\right) }\right) g+2 {{\omega }_{2}^{2}}\, {m_2} \sin{\left( {{\theta }_2}-{{\theta }_1}\right) } \mathit{L2}+{{\omega }_{1}^{2}}\, {m_2} \sin{\left( 2 {{\theta }_2}-2 {{\theta }_1}\right) } \mathit{L1}}{\left( {m_2} \cos{\left( 2 {{\theta }_2}-2 {{\theta }_1}\right) }-{m_2}-2 {m_1}\right) \, \mathit{L1}},{{\alpha }_2}=\frac{\left( \left( {m_2}+{m_1}\right) \sin{\left( {{\theta }_2}-2 {{\theta }_1}\right) }+\left( {m_2}+{m_1}\right) \sin{\left( {{\theta }_2}\right) }\right) g+{{\omega }_{2}^{2}}\, {m_2} \sin{\left( 2 {{\theta }_2}-2 {{\theta }_1}\right) } \mathit{L2}+\left( 2 {{\omega }_{1}^{2}}\, {m_2}+2 {{\omega }_{1}^{2}}\, {m_1}\right) \sin{\left( {{\theta }_2}-{{\theta }_1}\right) } \mathit{L1}}{\left( {m_2} \cos{\left( 2 {{\theta }_2}-2 {{\theta }_1}\right) }-{m_2}-2 {m_1}\right) \, \mathit{L2}}]]\]

These are exactly the final equations of motion presented in https://www.myphysicslab.com/pendulum/double-pendulum-en.html

2 The numerical solution

We will use the Runge-Kutta method. Here is a Maxima function that directly generates the
animation. Notice how we transform from the variables (%theta[1],%theta[2],%omega[1],%omega[2])
to (x1,y1,x2,y2) (and we only use (x,y) to actually represent the double pendulum):

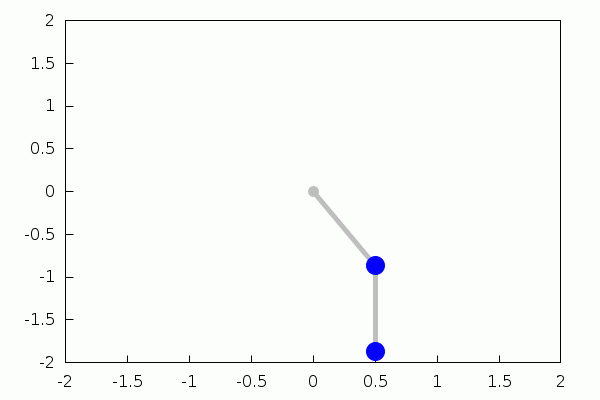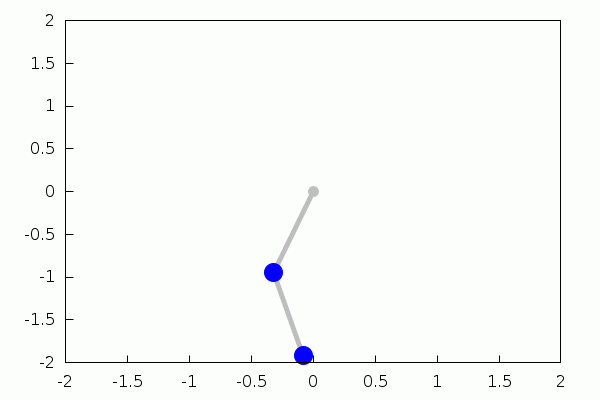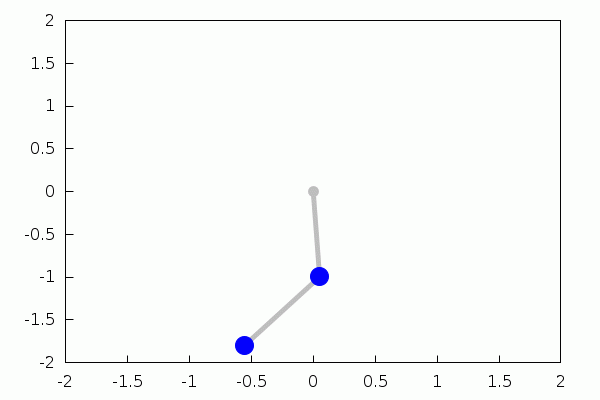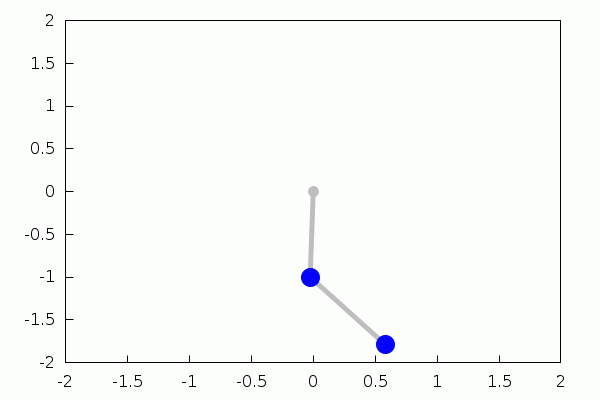
(%i21) double_pendulum(L1,L2,m1,m2,g,t10,t20,w10,w20,tspan,tstep,ff):=block(
[%theta1,%theta2,%omega1,%omega2,expr1,expr2,expr3,expr4,tmp,N,soln1,soln2,wxanimate_framerate:ff],
expr1:%omega1,
expr2:%omega2,
expr3:−((m2·sin(2·%theta2−%theta1)+(−m2−2·m1)·sin(%theta1))·g+2·m2·%omega2^2·sin(%theta2−%theta1)·L2+%omega1^2·m2·sin(2·%theta2−2·%theta1)·L1)/
((m2·cos(2·%theta2−2·%theta1)−m2−2·m1)·L1),
expr4:(((m2+m1)·sin(%theta2−2·%theta1)+(m2+m1)·sin(%theta2))·g+m2·%omega2^2·sin(2·%theta2−2·%theta1)·L2+(2·%omega1^2·m2+2·m1·%omega1^2)·sin(%theta2−%theta1)·L1)/
((m2·cos(2·%theta2−2·%theta1)−m2−2·m1)·L2),
tmp:rk([expr1,expr2,expr3,expr4],[%theta1,%theta2,%omega1,%omega2],[t10,t20,w10,w20],[t,0,tspan,tstep]),
N:length(tmp),
soln1:makelist([L1·sin(k[2]),−L1·cos(k[2])],k,tmp),
soln2:soln1+makelist([L2·sin(k[3]),−L2·cos(k[3])],k,tmp),
with_slider_draw(l,makelist(m,m,1,N),
xrange=[−L1−L2,L1+L2],
yrange=[−L1−L2,L1+L2],
point_type=filled_circle,
color=gray,
points([[0,0]]),
points_joined=true,
line_type=solid,
line_width=5,
points([[0,0],soln1[l]]),
points([soln1[l],soln2[l]]),
color=blue,
point_size=3,
points_joined=false,
points([soln1[l],soln2[l]])
)
)$

The syntax is more or less clear, but here are the details (in all cases, the subscript 1 refers
to the upper pendulum and 2 to the lower pendulum):
L1, L2 lengths of the rods,
m1, m2 masses of the bobs,
g value of gravitational constant,
t10, t20 initial values of the angular displacements (short for %theta1[0] and %theta2[0]),
w10, w20 initial values of the angular velocities,
tspan is the total time the animation will run,
tstep is the tiem step in the Runge-Kutta method (some value around 0.05 is enough),
ff is the animation framerate.

Here is an example:

(%i22) double_pendulum(1,1,2,2,9.8,%pi/6,0,0,0,5.5,0.05,17);
\[\tag{%t22} \] Animated Diagram \[\tag{%o22} \]
This document was created using wxMaxima, the nice tool in https://ezgif.com/speed, and heavy hand-editing.