Wave functions of the quantum oscillator

We will use some special functions (the Hermite polynomials) which are implemented in
Maxima's orthopoly package, so we first load it:

(%i1) load(orthopoly)$

Result

Now, let us write the wave functions which are solutions to the Schrödinger equation
for the potential mω2x2/2 (the harmonic oscillator). We will take m=1=h/2π and
ω=2 in what follows, for simplicity. Following eq. (4.10) in M. Chester's "A primer of
Quantum Mechanics", Dover 2003 (pg. 81), we have:

(%i2) %psi(n,x):=(%i)^n *exp(-x^2)*hermite(n,sqrt(2)*x)/sqrt(2^n *n!*sqrt(%pi/2));

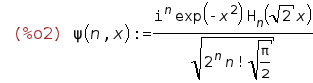
Result

Here n is the integer parametrizing the energy levels E=(n+1/2)2=2n+1 (with our values
for h and ω), see eq. (4-9) in the book. For instance, the wave function corresponding
to n=2 (E=5) is is:

(%i3) wxplot2d(%psi(2,x),[x,-5,5]);

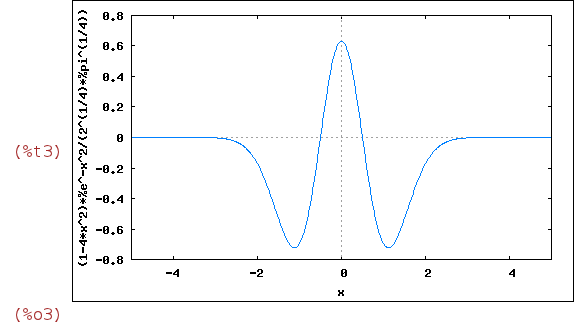
Result

Note that in Figure 4.2 of the book, it is -ψ(2,x) what is pictured. Now we show the
different energy levels on the same diagram, as in Figure 4.3 of Chester's book, shifting
the wave functions vertically so they sit at the energy level they represent:

(%i16) wxplot_size:[500,500];

Result

(%i17) with_slider(n,[0,1,2],
append([2*x^2,1,3,5],makelist((2*k+1+%i^(-1/2 +1/2*(-1)^k +2*k)*%psi(k,x)),k,0,n)),
[x,-2.25,2.25],[y,-0.25,10],[legend,2*x^2,E(n=0)=1,E(n=1)=3,E(n=2)=5,psi(0,x),psi(1,x),psi(2,x)]
);

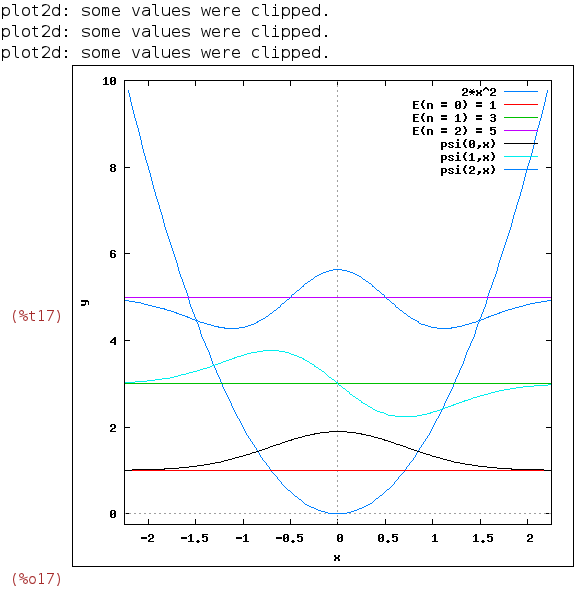
Result

A brief remark: note that Chester's book, Figure 4.3, displays the wave functions
ψ(0,x), iψ(1,x), ψ(2,x), and so on, while the formula for ψ(n,x) contains
a factor in, which alternates sign. It is to compensate this extra sign that we have
added the factor i-1/2 +(-1)k/2 +2k, which may seem strange at first sight.

Created with wxMaxima.