Sitio Web de Héctor E. Medellín Anaya
![]()
Sitio Web de Héctor E. Medellín Anaya
|
|
Cada día hábil después de la fecha de entrega baja un punto a la calificación de la tarea.
Tarea#1 (entrega: 24 - agosto - 2005) tarea de Matlab Tarea#2 (entrega: 31 - agosto - 2005) 1. Escriba una funcion que calcule el area de
un triangulo, pase como parametros la longitud de los lados.
4. Escriba un archivo M de función llamándolo
fun_es(x) para calcular: Escriba otro archivo M que lea dos valores desde el teclado y grafique la función fun_es entre esos dos valores. Utilice el comando fplot para hacer la gráfica.
Tarea #3 Entrega: miercoles 7 de septiembre de 2005 Problemas del libro de Burden pags. 53 y 54. Entregue un reporte que incluya solo la solución encontrada, el número de pasos que se hicieron, las fórmulas que escribio en Excel, el código en Matlab y las gráficas generadas. Utilice el tipo Courier New. 1. Aplique el método de la bisección para obtener p3 para f(x) = sqrt(x) - cos x en [0,1]. Grafique cada intervalo en Matlab. 2. Aplique el método de la bisección para encontrar las soluciones exactas en 10-2 para x3 - 7x2 + 14x - 6 = 0 en cada intervalo. Grafique cada intervalo en Matlab. a. [0, 1] b.[1, 3.2] c. [3.4, 4] 7. Aplique el método de bisección para encontrar soluciones exactas en 10–5 para los siguientes problemas. Grafique cada intervalo en Matlab. a. x – 2–x = 0 para 0 <= x <= 1 b. ex – x2 + 3x - 2 = 0 para 0 <= x <= 1 c. 2x cos(2x) - (x + 1)2 = 0 para –3 <= x <= –2 y para –1 <= x <= 0 d. x cos x - 2x2 + 3x – 1 = 0 para 0.2 <= x <= 0.3 y para 1.2 <= x <= 1.3
Tarea #4 Punto fijo, entrega: viernes 9 de septiembre de 2005 1. Use el manejo algeb raico para demostrar que las siguientes funciones tienen un punto fijo en p exactamente cuando f(p) = 0, donde f(x) = x4 + 2x2 – x –3 a. g1(x) = (3 + x – 2x2)1/4 b. g2(x) = ((x + 3 – x4)/2)1/2 c. g3(x) = ((x + 3)/(x2+2))1/2 d. g4(x) = (3x4 + 2x2 + 3)/(4x3 + 4x – 1) 2. a. Efectue cuatro iteraciones, si es posible, en las funciones g definidas en el ejercicio 1. Sea p0= 1 y pn+1 = g(pn) para n = 1, 2, 3, 4. b. ¿Cuál función, a su juicio, dará la mejor aproximación a la solución? 3. Aplique el método de iteración de punto fijo para determinar una solución exacta en 10-2 para x3 - x - 1 = 0 en [1, 2]. Utilice p0 = 1. Tarea #5 Método de Newton Raphson, entrega: lunes 19 de septiembre de 2005 1. Aplique el método de Newton para obtener soluciones con una exactitud de 10-4 para los siguientes problemas. a. x3 - 2x2 - 5 = 0, [1, 4] c. x - cos x = 0, [0, p/2] b. x3 + 3x2 - 1 = 0, [-3, -2] d. x - 0.8 - 0.2sen x = 0, [0, p/2] 2. Aplique el método de Newton para obtener soluciones con una exactitud de 10-5 para los siguientes problemas. a. ex + 2-x + 2cos x - 6 = 0 para 1<= x <= 2 b. ln(x - 1) + cos(x - 1) = 0 para 1.3<= x <= 2 c. 2x cos 2x - (x - 2)2 = 0 para 2<= x <= 3 y 3<= x <= 4 d. (x - 2)2 - ln x = 0 para 1<= x <= 2 y e<= x <= 4 e. ex - 3x2 = 0 para 0<= x <= 1 y 3<= x <= 5 f. sen x - e-x = 0 para 0<= x <= 1 y 3<= x <= 4 y 6<= x <= 7 3. Un objeto que cae verticalmente en el aire está sujeto a una resistencia viscosa y también a la fuerza de gravedad. Supongamos que dejamos caer un objeto de masa m desde una altura y0 y que la altura del objeto después de t segundos es y = y0 +m g t / k - m2 g / k2 (1 - e- k t / m) donde g = -32.17 pies/s2 y k representa la resistencia del aire. a) Escriba un programa en Matlab que lea y0 y m (suponga k=0.1 lb-s/pie) y calcule el tiempo de caida del objeto. b) Haga una hoja de Excel para resolver este problema, Utilice alguno de los métodos para solución de ecuaciones no lineales. 4. El medicamento administrado a un paciente produce una concentración en la corriente sanguinea dada por c(t) = Ate-t/3 miligramos por mililitro, t horas después de inyectarle A unidades. La máxima concentración inocua es de 1.00 mg/ml. a) ¿Qué dosis deberá inyectarsele al paciente para alcanzarla máxima concentración inocua y cuando se presenta ésta? b) Una cantidad adicional del medicamento deberá administrársele al paciente después de que la concentración disminuya a 0.25 mg/ml. Determine con una aproximación al minuto más cercano, cuándo debe aplicarsele la segunda inyección. c) Suponiendo que la concentración producida por inyecciones consecutivas es aditiva y que el 75% de la dosis inyectada originalmente se administra en la segunda inyección, ¿cuando será el momento de aplicarle la tercera inyección? Resuelva en Excel y en Matlab. Tarea #6 Ceros de polinomios entrega: 23 de septiembre de 2005 En cada caso reporte: el valor inicial que utilizó para x y los valores de x y del polinomio en cada iteración. Si hizo una gráfica para encontrar las raices reales, inclúyala en el reporte. NO IMPRIMA LA HOJA DE CÁLCULO. Para las raices complejas del problema 2, reporte las cuadráticas que obtuvo. 1. Obtenga las aproximaciones, con una exactitud de 10-4 a todos los ceros reales del siguiente polinomio aplicando el método de Newton. Utilice una hoja electrónica en Excel. a) P(x) = x3 - 2x2 - 5 b) P(x) = x3 + 3x2 - 1 c) P(x) = x3 - x - 1 d) P(x) = x4 + 2x2 - x - 3 e) P(x) = x3 + 4.001x2 + 4.002x + 1.101 f) P(x) = x5 - x4 + 2x3 - 3x2 +x - 4 2. Obtenga aproximaciones con un grado de exactitud de 10-5 a todos los ceros de los siguientes polinomios, encontrando primero los ceros reales mediante el método de Newton y reduciendo luego los polinomios de menor grado para determinar los ceros complejos. a) P(x) = x4 + 5x3 - 9x2 - 85x - 136 b) P(x) = x4 - 2x3 - 12x2 + 16x - 40 c) P(x) = x4 + x3 + 3x2 + 2x + 2 d) P(x) = x5 + 11x4 - 21x3 - 10x2 - 21x - 5 e) P(x) = 16x4 + 88x3 + 59x2 + 76x - 240 f) P(x) = x4 - 4x2 - 3x + 5 g) P(x) = x4 - 2x3 - 4x2 + 4x + 4 h) P(x) = x3 - 7x2 + 14x - 6 3. Repita el problema 2 usando el método de Müller. Proyecto Debemos construir una lata de forma cilíndrica que contenga 10000cm3. La tapa circular de la parte superior y del fondo deben tener un radio de 0.25 cm más que el radio de la lata, para que el sobrante se utilice para sellar con la parte lateral. La hoja de material con que se construye esta parte de la lata (las paredes del cilindro) deben ser 0.25 cm más grande que la circunferencia de la lata, de modo que pueda hacerse el sello. Cálcule, con una exactitud de 10-4 la cantidad de material necesario para fabricar la lata. Escriba un programa en Matlab que lea el volumen que se desea de la lata y calcule las dimensiones y la cantidad de material necesario para construirla. ¿las latas comerciales cumplen estas especificaciones? Repita la solución con una hoja de Excel 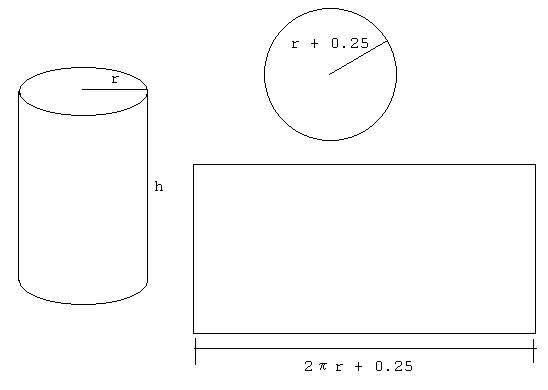
Tarea #7 Interpolación de Lagrange (entrega 14 de octubre de 2005) 1. Para las funciones dadas f(x), sea x0 = 0, x0 = 0.6, x0 = 0.9. Construya polinomios de interpolación de grados uno y dos a lo máximo para ´aproximar f(0.45), y calcule el error real. a. f(x) = cos (x) b. f(x) = ln(x + 1) c. f(x) = tan x 2. Construya los polinomios de interpolación de Lagrange de grado 2 y aproxime lo siguiente. Incluya en su reporte el polinomio de la forma ax2 + bx + c en cada caso. Haga una hoja de cálculo o un programa en Matlab para obtener el polinomio e incluyalo en el reporte. a. f(8.4) si f(8.1) = 16.94410, f(8.3) = 17.56492, f(8.6) = 18.50515. b. f(-1/3) si f(-0.75) = -0.071813, f(-0.5) = -0.02475, f(-0.25) = 0.3349375 c. f(0.25) si f(0.1) = -0.62049958, f(0.2) = -0.28398668, f(0.3) = 0.00660095 d. f(0.9) si f(0.7) = 0.01375227, f(0.8) = 0.22363362, f(1.0) = 0.65809197 3. Los datos del ejercicio anterior fueron calculados con las siguientes fórmulas. Calcule el error absoluto de las aproximaciones calculadas en cada caso. a) f(x) = x ln x b) f(x) = x3+4.001x2+4.002x+1.101 c) f(x) = x cos x-2x2+3x-1 d) f(x) = sen(ex - 2)
Tarea #8 (entrega: 20 de octubre de 2005) 1. Calcule la derivada de las siguientes funciones en los puntos inficados. Utilice el método de diferencia progresiva en Excel o Matlab. a. f(x) = 3sen(2px - p/6)e-x, x = 0.5 b. f(x) = esen(2x) - 5x2, x = 1.3 Tarea #9 (entrega: 24 de octubre de 2005) 1. Aproxime las siguientes integrales aplicando la regla del trapecio y la regla de Simpson.
2. Integre analíticamente las integrales del ejercicio 2 y calcule el error absoluto en cada caso. Haga una tabla con los resultados obtenidos. 3. Aproxime las siguientes integrales aplicando la regla compuesta del trapecio, la regla compuesta de Simpson y la regla compuesta del punto medio. Utilice los programas del problema 1.
4. Integre analíticamente las integrales del ejercicio 4 y calcule el error absoluto en cada caso. Haga una tabla con los resultados obtenidos.
Tarea #10 (entrega: 7 de noviembre de 2005) 1. Usa la eliminación gaussiana con sustitución hacia atrás y la aritmética de redondeo a dos dígitos para resolver los sistemas lineales siguientes. No reordene las ecuaciones. La solución exacta de cada sistema es x1 = 1, x2 = -1, x3 = 3. Haga todo el proceso a mano. 4x1 - x2
+ x3 = 8 4x1 + x2
+ 2x3 = 9 2. Resuelva los siguientes conjuntos de
ecuaciones por el método de Gauss en MATLAB 4x1 + x2
- x3 = 9 x1 +
x2 = 0 3. Dado el sistema lineal 2x1 - 6ax2
= 3 a. obtenga el valor o los valores de a para los cuales el sistema no tiene solución. b. obtenga el valor o los valores de a para los cuales el sistema tiene una cantidad infinita de soluciones. c. Suponinedo que existe una solución única para a encuentre la solución. Tarea#11: Algebra de matrices (entrega: miércoles 16 de noviembre) En todos los problemas, hagalos a mano y escriba un script en Matlab. 1. Sean las siguientes matrices | 2 0 5|
|-1 3 1 -4| calcule las siguientes expresiones: a) 2A, b) 3AB - 5B, c) B - AB, d) AAA 2. Encuentre la inversa de la siguiente matriz usando eliminación de Gauss. Calcule AT, encuentre la inversa de AT y muestre que se cumple: (AT)-1 = (A-1)T |4 2 -3| 3. Calcule el determinante de las siguientes matrices convirtiendo en una matriz triangular. | 2 0 5|
| 1 1 -1 1|
Tarea#12: Normas (entrega: viernes 25 de noviembre) 1. Obtenga || x ||2 y || x ||¥para los siguientes vectores a. x = (3, -4, 0, 3/2)t b. x = (2, 1, -3, 4)t c. x = (4/(k + 1), 2/k2, k2e-k)t 2. Demuestre que las siguientes sucesiones son convergentes y encuentre su límite. a. x(k) = (1/k, e1- k, -2/k2)t b. x(k) = (e-kcos k,k sen(1/k), 3 + k -2)t 3. Obtenga || . ||¥ para las matrices siguientes |4 2 -3| | 2 -1 0| | 4 -1 7| Tarea#13: Métodos iterativos (entrega: miércoles 18 de mayo) 1. Obtenga las dos primeras iteraciones del método iterativo de Jacobi para los siguientes sistremas lineales, usando x(0) = 0. Haga sus cálculos en forma manual (con calculadora) con 5 dígitos de precisión. 3x1 - x2 + x3
= 1 10 x1
- x2 = 9 10 x1 + 5 x2
= 6
4x1 + x2 - x3 + x4 = -2 4 x1 + x2 +
x3 + x5 = 6
4x1 - x2
- x4
= 0 2. Repita el problema anterior con el método de Gauss-Seidel. 3. Aplique el método de Jacobi para resolver los sistemas lineales del problema 1, con TOL = 10-3 en la norma l¥. Utilice Excel para hacer sus cálculos. Imprima solo la solución a la que llegó y el número de iteraciones. 4. Repita el problema 3 con el método de Gauss-Seidel. 5. Escriba un programa en Matlab para resolver un sistema de ecuaciones utilizando el método de Jacobi y el método de Gauss-Seidel. Tercer examen parcial. Fecha de entrega: viernes 2 de diciembre. 1. Utilice las funciones MINVERSA y MMULT de Excel para resolver los siguientes sistemas de ecuaciones. Lea con atención la ayuda de Excel para utilizar estas funciones. Note que la matriz del sistema es la misma y solo cambian los términos independientes. 2x1 + 2x2 - 2x3 = 3
2x1 + 2x2 - 2x3 = 1 2x1 + 2x2 - 2x3 = 2
2x1 + 2x2 - 2x3 = -5 2. Resuelva el siguiente sistema utilizando el método de Jacobi o el de Gauss Seidel con una tolerancia de 10-3 en la norma l¥. Inicie con el vector 0. Haga un script en Matlab para este problema o resuelvalo en Excel. 2x1 + x2 - x3
= 3
|