"DIALOGOS CONCERNIENTES A DOS
CIENCIAS NUEVAS" (LA MECANICA Y LA BALISTICA)


Galileo Galilei (1564 - 1642)
En 1492, Colón descubrió un mundo nuevo; en 1610
Galileo, italiano también, aunque más grande que Colón como hombre de ciencia,
descubrió un cielo nuevo, cuyas profundidades no se han explorado aún del todo.
Asestando al cielo de una noche despejada el telescopio construido con sus propias
manos, el matemático florentino fue el primer hombre que contempló el aspecto
verdadero de la luna, el primero que descubrió, a inmensa distancia encima de su
frente más miradas de lo que habían soñado todos los filósofos. Allí estaba el
anhelado mensaje de las estrellas, dado a conocer en "El Mensajero Sideral";
allí la confirmación visible de la astronomía copernicana, valientemente propugnada
por Galileo, quedaba patente ante los ojos de todos los inquisidores romanos que se
atreviesen a mirar.
A la visión de los cielos añadió el perseguido
"caballero andante de la ciencia" la visión de la tierra, no menos
perturbadora para los eclesiásticos empecinados en defender los errores de
Aristóteles. Despertado a la ciencia por la observación que hizo en su adolescencia
de las lámparas que en la catedral de Pisa se balanceaban con movimiento pendular,
convencido por los experimentos prolijamente planeados que hizo con piedras de
diferentes pesos que caían en tiempos iguales de lo alto de la torre inclinada de la
misma ciudad, fue Galileo el primero que conoció y expresó con toda claridad la ley
fundamental de la dinámica y la balística, las dos "ciencias nuevas" por
él fundadas; a saber, que no es el movimiento mismo sino el "cambio" de
movimiento lo que exige la aplicación de una fuerza nueva. Quedaba reservado para
Newton el explicar los pormenores lo que sucede cuando dicha fuerza es la gravedad.
La lengua empleada ordinariamente por Galileo es el
italiano. La traducción inglesa de "El mensajero sideral" (obra escrita en
latín) es obra de Edward Stafford Carlos (1880). Los pasajes entresacados de
"Diálogos acerca de dos ciencias nuevas" fueron traducidos por Henry Crew y
Alfonso de Salvio, publicados con dicho título (Dialogues Concerning Two New
Sciences) en 1914 por la Macmillan Company, y reimpresos en 1939 por la Junta Editora
de los Estudios Universitarios del Noroeste (Editorial Board of Northwestern
Universities Studies).

INTERLOCUTORES: SALVIATI, SAGREDO Y SIMPLICIO
Salviati: La constante actividad que
desplegáis vosotros, los venecianos, en vuestros famosos arsenales, señala al
entendimiento estudioso vasto campo de indagaciones, en particular aquella porción de
las obras que exigen mecánica; porque en dicha sección de continuo fabrican toda
suerte de aparatos y máquinarias, numerosos artesanos entre los cuales debe de haber
quienes, en parte por la experiencia heredada y en parte merced a sus propias
observaciones, han adquirido gran pericia e inteligencia en la explicación de las
cosas.
Sagredo: Tenéis sobrada razón. Tanto,
que yo mismo, curioso como soy por naturaleza, a menudo visito este lugar, por el solo
gusto de observar la faena de aquellos a quienes, por su superioridad sobre los demás
artesanos, denominamos "hombres de primera categoría"...
LA VELOCIDAD DE LA LUZ
Salviati: Observamos que las demás
combustiones y resoluciones van acompañadas de movimiento, y rapidísimo. Parad
mientes, si no, en la acción de encenderse la pólvora, tal como suele hacerse en las
minas y petardos; advertid además cómo la llama del carbón de piedra, a pesar de
hallarse mezclada con exhalaciones pesadas e impuras, aumenta su poder de derretir
metales, avivándola un par de fuelles. Por eso no entiendo cómo la acción de la
luz, aunque purísima, puede estar desprovista de movimiento, y movimiento
velocísimo.
Simplicio: La experiencia de cada día
nos enseña que la propagación de la luz es instantánea; porque, cuando vemos
disparar de muy lejos una pieza de artillería, el chispazo nos llega a los ojos, sin
que transcurra tiempo; y, en cambio, el sonido no llega a nuestros oídos sino tras un
intervalo perceptible.
Sagredo: Bueno, Simplicio, lo único que
puedo inferir de esa experiencia tan conocida es que el sonido, para llegar a nuestros
oídos, tarda más que la luz; pero no me dice si la venida de la luz es instantánea
o si, aunque rapidísima, ocupa tiempo. Esta suerte de observaciones no nos enseña
más que aquello de que "en llegado el sol al horizonte, nos llega su luz a los
ojos"; pues, ¿quién me asegura que los tales rayos no han llegado al sobredicho
límite antes de llegar a nuestra vista?
Salviati: Lo escaso de la fuerza
probatoria así de estas observaciones como de otras por el estilo me indujo en cierta
ocasión a elucubrar un método mediante el cual pueda uno averiguar con certidumbre
si es en verdad instantánea la iluminación, o sea, la propagación de la luz. El que
la velocidad del sonido sea tan grande como lo es, nos da la certeza de que el
movimiento de la luz no puede menos de ser velocísimo. He aquí el experimento que se
me ocurrió.
Cada una de dos personas cogerá una luz metida dentro
de una linterna u otro receptáculo, tal que una de dichas personas, poniéndole
delante la mano o quitándosela, impida que pase la luz o la deje pasar hasta los ojos
de la otra. Luego se pondrán una frente a la otra, a unos cuantos codos de distancia,
y se ejercitarán, hasta adquirir tanta habilidad en descubrir y ocultar sus luces,
que en el instante en que viere uno la luz de su compañero descubra la suya. Tras de
algunos ensayos la respuesta será tan pronta, que el descubrirse de una luz seguirá
al punto el descubrirse de la otra; de suerte que, en descubriendo uno su luz, verá
al instante la luz del otro. Habiendo adquirido su pericia a corta distancia, los dos
experimentadores, aparejados como antes, ocuparán posiciones separadas entre sí por
una distancia de dos o tres millas, y efectuarán el mismo experimento de noche,
fijándose con todo cuidado en si las apariciones y eclípses acaecen del mismo modo
que a distancias breves; si tal sucede, podremos afirmar con toda seguridad que la
propagación de la luz es instantánea; pero si, a una distancia de tres millas, que
en realidad, teniendo en cuenta la ida de una luz y la venida de la otra, es de seis,
exige tiempo, en tal caso la demora ha de poderse observar con facilidad. De hacerse
este experimento a distancias aún mayores, de ocho a diez millas, pongo por caso,
pueden emplearse telescopios colocando el suyo cada observador en el lugar donde haya
de hacer su experimento de noche. Entonces, aun cuando las luces fueren pequeñas y,
por ende, imperceptibles a simple vista, podrán descubrirse y cubrirse con
expedición, ya que, puestos y asestados los telescopios merced a ellos fácilmente se
verán las luces.
Sagredo: Parece el tal experimento
invención ingeniosa y expedita. Mas decidnos a que conclusión os llevan los
resultados.
Salviati: En realidad, no he ensayado el
experimento sino a distancia breve, de menos una milla; por lo cual no he podido
averiguar a punto fijo si la aparición de la otra luz era o no instantánea. Pero de
no ser instantánea, es extraordinariamente rápida, momentánea, por decirlo así. Y
por lo pronto compararía yo su movimiento con el que vemos en el relámpago que
estalla entre nubes, a ocho o diez millas de nosotros. Vemos el comienzo de dicha luz,
su fuente y cabeza, por decirlo así, en algún sitio particular entre las nubes; pero
enseguida se propaga a los que lo rodean; lo cual parece probar que para la
propagación se requiere cuando menos algún tiempo. Porque, si la iluminación no
fuese paulatina sino instantánea, no se podría distinguir su origen, su centro, por
decirlo así, de sus partes exteriores. ¡En que mar nos vamos deslizando sin
percatarnos de ello!. Con vacíos e infinidades de movimientos individuales e
instantáneos, ¿podemos alguna vez, aun después de disputas infinitas, llegar a
tierra firme?
Sagredo: En verdad estas materias muy
lejos quedan de nuestro alcance. Pensemos tan sólo que buscando sobre los números lo
infinito, damos con la unidad; que los siempre divisibles se derivan de los
indivisibles; el vacío se halla inseparablemente unido a lo lleno. En efecto, las
opiniones que de ordinario se tienen acerca de la naturaleza de estas materias son tan
enrevesadas que hasta la circunferencia del círculo viene a parar en una recta
infinita. . .
¿CON QUE CELERIDAD CAE LA PIEDRA?
Simplicio:
Admirable, en verdad, es vuestro discurso; empero, no se me hace fácil creer que el
pájaro herido de un disparo caiga con la misma rapidez que una bala de cañón.
Salviati: ¿Por qué no decir que un
grano de arena cae con la misma velocidad que una piedra de molino? . Pero, Simplicio,
espero que no seguiréis el ejemplo de tantos otros, que, desviando la controversia de
su principal intento, se valen de alguna afirmación mía a la cual falta el grueso de
un cabello para llegar a la verdad, y con este cabello esconden la falta de otra,
gorda como cable de navío? Dice Aristóteles que "una pelota de hierro de cien
libras de peso, que cae de cien codos de altura, llega al suelo antes que una pelota
de una libra que haya caído de un codo"; yo afirmo que ambas llegan al mismo
tiempo.
Hallaréis, haciendo la prueba, que la pelota más
grande llevará dos dedos de ventaja a la más pequeña, o sea, que cuando la mayor
hubiere llegado al suelo, a la menor le faltan dos dedos para llegar. Ahora bien, no
esconderéis detrás los noventa y nueve codos de Aristóteles, ni haréis hincapié
en mi leve error, pasando por alto el grandísimo suyo. Declara Aristóteles que
cuerpos de peso diferente se mueven dentro de un mismo medio (en cuanto su movimiento
depende de su gravedad) con velocidades proporcionales a sus pesos respectivos; lo
cual ilustra echando mano de cuerpos con los cuales es dado percibir los efectos de la
gravedad puros y sin adulteración, eliminando otras consideraciones, como, por
ejemplo, la figura, a fuera de influjos poco importantes, que dependen en gran manera
del medio que modifica únicamente el efecto de la sola gravedad.
Así observamos cómo el oro, que es la más densa de
todas las sustancias, flota en el aire, si lo reducimos a lámina muy delgada; lo
mismo acontece con la piedra molida hasta convertirse en polvo muy menudo. Pero si
quisiereis sostener la proporción general, tendréis que demostrar que la misma
relación de velocidades se conserva en el caso de todos los cuerpos pesados, y que
una piedra de veinte libras se mueve diez veces más aprisa que una piedra de dos;
pero yo aseguro que ello es falso, y que, si cayesen de cincuenta o cien codos de
altura, llegarían simultáneamente a la tierra.
Simplicio: Acaso el resultado sería
diferente, si la caída se hiciese, no ya desde unos cuantos codos, sino desde miles
de codos.
Salviati: Si tal quisiese decir
Aristóteles, le echaríais a cuestas otro error, que llegaría a falsedad; porque, no
pudiendo disponerse en la tierra de tan descomunal altura, claro está que
Aristóteles no pudo hacer semejante experimento; y, no obstante, desea dejarnos la
impresión de que lo llevó a cabo, hablando de tal efecto como de cosa que vemos.
Simplicio: En realidad Aristóteles no se
vale de este principio, sino emplea el otro, que, según creo yo, no da pie a las
mismas dificultades.
Salviati: Pero éste es tan falso como
aquel; y me asombra el que no veais la falacia ni os percatéis de que, a ser verdad
que en medio de densidades y resistencias diferentes, como el agua y el aire, el mismo
cuerpo se mueve con más rapidez en el aire que en el agua, según la proporción en
que la densidad del agua es mayor que la del aire, se seguiría que todo cuerpo que
cae a través del aire también debería caer a través del agua. Pero tal cosa es
falsa, ya que muchos cuerpos que bajan por el aire no sólo bajan en el agua, sino se
levantan en ella.
Simplicio: No comprendo la necesidad
lógica de vuestra conclusión; y, a mayor abundamiento diré que Aristóteles trata
únicamente de los cuerpos que caen en ambos medios, y no de los que caen en el aire y
suben en el agua.
Salviati: Los argumentos que en pro de
los filósofos traéis a colación son tales que el mismo Aristóteles los habría
rechazado ciertamente, para no agravar más aún su error primero.
ENVIDIA
Simplicio: A mi parecer, los argumentos
anteriores dejaban algo que desear; pero ahora me doy por el todo satisfecho.
Salviati: Los hechos que hasta ahora he
traído a colación y en particular el que hace ver cómo la diferencia de los pesos,
por muy grande que fuera, no produce efecto alguno en el cambio de velocidad de los
cuerpos que caen, de suerte que, en cuanto se refiere al peso, todos ellos caen con
igual velocidad, esta idea, digo, es tan nueva y, al parecer, tan ajena de la
realidad, que, de no disponer de medios de hacerla tan clara como el sol, más valiera
no haberla mencionado; pero, ya que le permití salir de mis labios, no he de omitir
experimento ni argumento alguno para corroborarla.
Sagredo: No sólo esta opinión vuestra,
sino muchas otras son tan ajenas a las doctrinas y pareceres comúnmente admitidos,
que, si las publicaseis, os acarrearíais gran número de adversarios; porque la
naturaleza humana es de tal suerte, que los hombres no miran con buenos ojos los
descubrimientos, verdaderos o falsos, que se hacen en su propio terreno, cuando los
hacen otros distintos de ellos. Tachan al tal de novador en achaque de doctrina,
título poco grato, mediante el cual esperan cortar el nudo que no pueden desatar; y
se empeñan en destruir con minas subterráneas los edificios que alarifes pacienzudos
han construido con las herramientas acostumbradas. Mas, para nosotros, que no tenemos
pensamiento de ese jaez, son del todo satisfactorios los experimentos y argumentos que
hasta ahora habéis presentado.
HUESOS GIGANTESCOS
Por lo ya demostrado, fácilmente podréis ver la
imposibilidad de aumentar el tamaño de las estructuras, hasta darles grandes
dimensiones, así en la naturaleza como en el arte. Asimismo, la imposibilidad de
construir palacios, barcos o templos de enorme tamaño, de suerte que queden trabados
unos con otros sus remos, vergas, baos y pernos de hierro y, en suma, todas sus
partes; ni puede la naturaleza producir árboles de tamaño extraordinario, porque las
ramas se quebrarían por su mismo peso. Del mismo modo, imposible sería edificar las
estructuras óseas de los hombres, caballos y demás animales de manera que quedasen
trabadas y cumpliesen sus funciones ordinarias si dichos animales tuvieran que
aumentar enormemente en estatura; porque este aumento de estatura no puede lograrse
sino empleando un material más duro y fuerte que el de costumbre o agrandando el
tamaño de los huesos, y cambiándoles así la figura, hasta que la forma y aspecto de
los animales hiciese pensar en monstruos. Tal vez esto es lo que tuvo presente nuestro
discreto poeta, cuando, describiendo un desaforado gigante:
Calcularle la talla es
imposible:
Tan fuera de medida es su
tamaño. 1
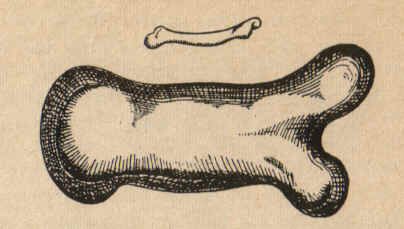
Para ponerlo ante los ojos, he dibujado un hueso cuyo
largo natural se ha triplicado y cuyo grosor se ha multiplicado de suerte que, para un
animal de tamaño proporcionalmente grande, pueda desempeñar la misma función que el
hueso pequeño cumple para su animal pequeño también. Por las figuras que aquí se
muestran, podréis ver cuán desproporcionado parece el hueso que se agrandó. Es, por
lo tanto, cosa manifiesta que si uno deseare conservar en un gran gigante la misma
proporción de miembros que se halla en un hombre ordinario, o bien tendrá que
descubrir un material más fuerte y resistente para fabricar los huesos, o bien
consentir en una disminución de robustez, si se le compara con los hombres de talla
mediana; porque, de aumentársele inconsiderablemente la talla, se desplomará y
quedará aplastado por su propio peso. Por el contrario, si se disminuye el tamaño de
un cuerpo; pues, en efecto, cuanto más pequeño fuere un cuerpo, tanto mayor será su
vigor relativo. Así, un perro pequeño podría probablemente llevar encima del lomo
dos o tres perros de su mismo tamaño; pero no creo que un caballo pudiera llevar ni
siquiera uno de su tamaño.
1(Ariosto,
Orlando furioso, XVII, 30.)
Simplicio: Puede que así sea; pero me
inclina a ponerlo en duda el tamaño enorme que alcanza cierto pez por el estilo de la
ballena; que, según tengo entendido, es diez veces más grande que un elefante y, sin
embargo, todos ellos se sostienen a sí mismos.
Salviati: Vuestra observación,
Simplicio, me hace pensar en otro principio en el que hasta ahora no había parado
mientras y que da a los gigantes y otros animales de enorme tamaño la posibilidad de
sostenerse a sí mismos y moverse de una parte a otra lo mismo que los animales más
pequeños. Puede obtenerse tal resultado, bien aumentando la fuerza de los huesos y
demás partes destinadas a llevar no sólo su propio peso, sino la carga
sobreañadida, o bien manteniendo constantemente las proporciones de la armazón
ósea; el esqueleto se sostendrá del mismo modo y hasta con mayor facilidad, con tal
que se disminuya en la misma proporción el peso del material óseo o de la carne y
todo lo demás que el esqueleto tenga que llevar. Este segundo principio es el que
emplea la naturaleza en la estructura del pez, haciéndole los huesos y músculos no
sólo livianos, sino por completo desprovistos de peso.
Simplicio: Salta a la vista el sesgo de
vuestra argumentación, Salviati. Puesto que el pez vive en el agua, la cual, por su
densidad o, como dirían otros, por su pesantez, disminuye el peso de los cuerpos
sumergidos en ella, queréis decir que por esta razón los cuerpos de los peces
estarán desprovistos de peso, y se sostendrán sin daño de sus huesos. Empero, esto
no basta; porque, aun cuando no pese lo demás del cuerpo del pez, no cabe duda sino
que los huesos le pesan. Consideremos, por ejemplo, una costilla de ballena que tenga
las dimensiones de un bao: ¿quién podrá negar que pesa mucho y que tiende a irse a
pique, si se la pone en el agua? Por tanto, difícilmente podría esperarse que moles
grandes se sustenten a sí mismas.
Salviati: ¡Agudísimo reparo, a fe mía!
Más ahora, por vía de respuesta, decidme si habéis visto alguna vez peces que a su
antojo se estén quedos dentro del agua, sin bajar hasta el fondo ni subir a la
superficie, absteniéndose de gastar fuerzas en nadar.
Simplicio: Es un fenómeno harto sabido.
Salviati: Pues, el que los peces puedan
estarse inmóviles debajo del agua es una razón decisiva para pensar que la materia
de sus cuerpos tiene la misma gravedad específica que el agua, y, por consiguiente,
si en su estructura hay ciertas partes más pesadas que el agua, ha de haber otras
más livianas que ésta, pues de otra suerte no producirían equilibrio.
Luego, si son pesados los huesos, es menester que los
músculos u otros constitutivos del cuerpo sean más livianos, para compensar con su
ligereza el peso de los huesos. Por consiguiente, hemos de dejar de maravillarnos de
que esos animales enormemente grandes moren en el agua más bien que en la tierra, o
sea, en el aire.
Simplicio: Quedo convencido; y sólo
deseo añadir que los que llamamos animales terrestres deberían llamarse en realidad
animales aéreos, puesto que en el aire viven, del aire están rodeados y respiran
aire.
Sagredo: Me ha complacido el discurso de
Simplicio, incluyendo así la pregunta suscitada como la respuesta. Además, entiendo
fácilmente que, de vararse en la playa uno de esos peces gigantes, quizá no se
sostendría largo tiempo, sino quedaría aplastado por su propia mole, en aflojándose
las trabazones de los huesos.
Salviati: Me inclino en favor de vuestra
opinión; y, en efecto, casi creo que sucedería lo mismo en el caso de un navío muy
grande que flotase en el mar sin desplazarse con el peso de su carga y armamento y que
en tierra firme y en el aire probablemente se desencuadernaría.
EL CAMBIO DE LUGAR
[ Habla
aquí el propio Galileo ]
Mi intento es exponer una ciencia muy nueva que trata
de un asunto muy viejo. No existe en la naturaleza nada más viejo que el movimiento,
acerca del cual los filósofos han escrito libros que no pecan de escasos ni de
pequeños. Sin embargo, mediante la experimentación he descubierto algunas
propiedades de él dignas de conocerse y hasta ahora nunca observadas ni demostradas.
Se han hecho, por ejemplo, algunas observaciones someras de que el movimiento libre de
un cuerpo pesado que cae tiene aceleración continua; pero hasta ahora no se ha
formado con exactitud el ámbito de tal aceleración; pues, que yo sepa, nadie ha
señalado que las distancias que en intervalos iguales de tiempo recorre un cuerpo que
parte del estado de reposo guardan con las de otro la misma proporción que los
números impares, comenzando por la unidad.
Se ha observado que los dardos y las balas recorren
cierta especie de trayectoria curva; pero nadie ha enunciado que la tal trayectoria es
una parábola. He logrado probar así esta verdad como otras no escasas en número ni
menos dignas de conocerse; y, lo que juzgo más importante aún, con ello se ha
abierto a esta vasta y excelentísima ciencia, de la cual mis trabajos no pasan de ser
un comienzo, caminos y vías merced a las cuales otras inteligencias más sagaces que
la mía exploran sus rincones remotos.
La primera parte de nuestro discurso trata del
movimiento uniforme o constante; la segunda, del movimiento que hallamos en la
naturaleza acelerado; la tercera trata de los llamados movimientos violentos y de los
cuerpos arrojadizos.
El movimiento uniforme: Al tratar del movimiento
uniforme hemos menester una definición, que hoy doy como sigue:
Definición: Por movimiento uniforme o
constante, entiendo aquel en el cual son iguales las distancias recorridas en
intervalos iguales por la partícula que se mueve.
EL EXPERIMENTO DE LA BOLA RODANTE
Salviati: Se cogió un trozo de madera
escuadrado, de unos doce codos de largo, medio codo de ancho y tres dedos de espesor;
en una cara se le abrió una canaleta de poco más de un dedo de ancho; habiendo hecho
esta ranura muy recta, lisa y pulida, y revestídola de pergamino también lo más
liso y terso posible, echamos a rodar por ella una bola de bronce dura, lisa y muy
redonda. Puesta la tabla en posición inclinada, alzándole un extremo a uno o dos
codos sobre el nivel del otro, echamos a rodar la bola por la ranura, como lo acabo de
decir, y anotamos, del modo que enseguida se describirá, el tiempo necesario para la
bajada. Repetimos este experimento más de una vez, a fin de medir el tiempo con
exactitud tal, que la diferencia entre dos observaciones no excediese nunca a la
décima parte de un latido del pulso. Efectuada esta operación y habiendo adquirido
certeza de lo seguro de ella, hicimos que la bola recorriese tan sólo la cuarta parte
del largo de la ranura; y, medido el tiempo de la bajada, hallamos que era cabalmente
un cuarto del de la bajada anterior. Hicimos la prueba con otras distancias, cotejando
el tiempo empleado por la bola en recorrer la longitud entera con el empleado en
recorrer la mitad, los dos tercios o cualquier otra fracción de ella; y en tales
experimentos, repetidos más de cien veces, siempre hallamos que los espacios
recorridos eran entre sí como de los cuadrados de los tiempos, y que esto era verdad
para todas las inclinaciones del plano, o sea, de la ranura por donde rodaba la bola.
También observamos que los tiempos de bajada para diversas inclinaciones del plano
guardaban entre sí cabalmente la proporción que, como más adelante veremos, el
autor les había previsto y demostrado.
Para medir el tiempo empleamos una vasija grande de
agua, puesta en un punto elevado; al fondo de esta vasija se soldó un tubo de
diámetro pequeño por donde salía un hilillo de agua que recogíamos en un vasito
durante el tiempo de cada bajada, así para todo lo largo de la ranura como para una
parte de la longitud de ésta; el agua recogida de esta suerte se pesaba, después de
cada bajada, en una balanza muy precisa; las diferencias y proporciones de esos pesos
nos dio las diferencias y proporciones de los tiempos, con tal exactitud que aun con
la operación se repitió una y otra vez, no hubo discrepancia apreciable en los
resultados.
Simplicio: Me hubiera gustado hallarme
presente a esos experimentos; pero confiado en el esmero con que los llevasteis a
efecto y en la fidelidad con que los referís, me doy por satisfecho y los recibió
por válidos y verdaderos.
Del libro Autobiografía de la ciencia de Forest
Ray Moulton y Justus J. Schifferes (Traducción de Francisco A. Delpiane).
![]()