EL SEGUNDO PRINCIPIO DE LA TERMODINAMICA


Rudolf Julius Emanuel Clausius
Físico Alemán que nació en Köslin, Pomerania
(ahora Koszalin, Polonia) el 2 de enero de 1822 y murió en Bonn el 24 de agosto de
1888.
Clausius fue principalmente un físico teórico,
ya que se dedicó a explicar las observaciones y experimentos efectuados por otros.
Sus trabajos versaron principalmente sobre física molecular y termodinámica. Fue
profesor de las universidades de Berlín, Zurich y Bonn.

Presentaremos a continuación un breve resumen de su trabajo.
Cuando un cuerpo cualquiera cambia de volumen, al mismo tiempo, por
regla general, se produce o consume trabajo mecánico. Pero en la mayoría de los
casos no es posible determinar éste con exactitud, porque junto con el trabajo
exterior se produce también comúnmente un trabajo interior desconocido. Para sortear
este inconveniente, Carnot empleó el ingenioso método, ya mencionado anteriormente,
de hacer experimentar al cuerpo diferentes transformaciones consecutivas, ordenadas de
tal manera que al final vuelva exactamente a su estado primitivo. Entonces, si en
alguna de las transformaciones se ha realizado trabajo interior, éste debe de quedar
exactamente anulado por el de las otras, y se tendrá la seguridad de que el trabajo
exterior que eventualmente se produzca en las transformaciones será también el
trabajo total. Clapeyron ha representado muy claramente este método en forma
gráfica, y nosotros utilizaremos por ahora esta representación para los gases
permanentes, si bien con una pequeña modificación, condicionada por nuestro
principio.
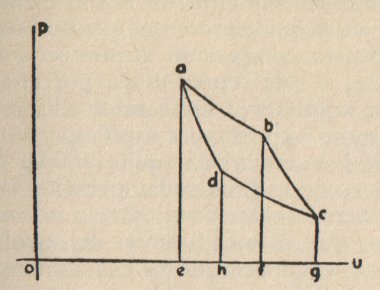
FIGURA 1
En la adjunta figura la abscisa oe representa el volumen, y la
ordenada ea la presión de la unidad de peso de un gas, en un estado cuya temperatura
sea igual a t. Admitamos ahora que el gas se encuentra en un recipiente
dilatable, pero con el cual no pueda, sin embargo, intercalar calor. Entonces, si lo
dejamos dilatar en este recipiente, y no le comunicamos nuevo calor, su temperatura
disminuirá. Para evitar esto, pongámoslo en contacto, durante la dilatación, con un
cuerpo A, manteniéndolo a temperatura constante, y que le comunique
siempre al gas la cantidad de calor necesaria para que su temperatura permanezca
igualmente con el valor f. Durante esta dilatación a temperatura
constante la presión disminuye de acuerdo con la ley de Mariotte, y la podemos
representar por las ordenadas de la curva ab, que es un segmento de
hipérbola equilátera. Cuando el gas aumente de volumen, en esta forma desde oe
hasta of, quitemos el cuerpo A, y, sin que pueda recibir
más calor, dejemos continuar la dilatación. Entonces la temperatura descenderá y
por lo tanto la presión disminuirá más rápidamente que antes; la ley según la
cual esto ocurre está representada por la curva bc. Una vez que el
volumen ha aumentado de of a og, con lo cual su
temperatura ha descendido de t hasta r comencemos a
comprimirlo nuevamente para llevarlo a su volumen inicial oe. Si al
hacer esto lo abandonamos a sí mismo, su temperatura aumentará de nuevo enseguida.
Pero por el momento no permitamos que esto suceda, poniéndolo en contacto con el
cuerpo B de la temperatura constante r, la cual transmite
de inmediato el calor producido, de modo que mantiene la temperatura r:
en esta forma comprimámoslo (en un intervalo gh) hasta que el segmento
restante le alcance exactamente para que su temperatura aumente de r a t,
cuando esta última compresión se efectúe de modo tal que no pueda ceder calor.
Durante la primera compresión la presión aumenta según la otra
hipérbola equilátera. En cambio, durante la última el aumento se produce con mayor
rapidez, y está representado por la curva da. Esta curva tiene que
terminar exactamente en a, puesto que, como al final de la operación la
temperatura y el volumen tienen su valor primitivo, lo mismo debe suceder con la
presión, que es una función de aquellas dos. Por lo tanto, el gas se encuentra ahora
exactamente en el mismo estado que al principio.
Para determinar ahora el trabajo producido en estas
transformaciones, por las razones expuestas sólo tenemos que concentrar la atención
en el trabajo exterior. Durante la dilatación el gas produce un trabajo que está
determinado por el integral del producto entre el diferencial de volumen y el valor
correspondiente de la presión, y que por lo tanto está representado geométricamente
por los cuadriláteros eafb y fbcg. Por el contrario, En
la compresión se consume trabajo, que está representado por del mismo modo por los
cuadriláteros gcdh y bdae. El exceso del primer trabajo
sobre el último debe considerarse como el trabajo total producido durante las
transformaciones y está representado por el cuadrilátero abcd.
Si todo el proceso antes descrito se realiza en orden inverso, se
obtiene la misma cantidad abcd como exceso del trabajo consumido sobre
el producido.
CONSECUENCIAS DEL PRINCIPIO DE CARNOT
Carnot ha supuesto que a la producción de trabajo le corresponde un
mero pasaje de calor de un cuerpo caliente a otro frío, sin que la cantidad de calor
disminuya en dicho pasaje.
La última parte de esta hipótesis, a saber, que la cantidad de
calor no resulta disminuida, contradice nuestro principio anterior y, por lo tanto, si
queremos conservar éste, debe de ser rechazada. La primera parte, en cambio, puede
mantenerse atendiendo a su contenido esencial. Puesto que, si bien ya no necesitamos
más un equivalente propio para el trabajo producido, desde que hemos admitido como
tal un consumo real de calor, es todavía posible, sin embargo, que aquel pasaje se
produzca simultáneamente con el consumo, y asimismo que esté en relación
determinada con el trabajo. Se trata, pues, de investigar si esta hipótesis además
de su posibilidad, tiene también de suyo una probabilidad suficiente.
Un pasaje de calor de un cuerpo caliente a otro frío ocurre
positivamente en aquellos casos en que se produce trabajo por acción del calor y al
mismo tiempo se cumple la condición de que la sustancia que interviene se encuentre
de nuevo al final en el mismo estado que al principio. En los procesos descritos
anteriormente, y representados en la figura citada, hemos visto que el gas y el agua
que se vaporiza recibían calor del cuerpo A al aumentar de volumen, y
que daban calor al cuerpo B durante la disminución de volumen, de tal
modo, pues, que una determinada cantidad de calor ha sido transportada de A
a B, y que ésta era, además, mucho mayor que la que admitimos como
consumida, de manera que en las transformaciones infinitamente pequeñas que están
representadas en la figura, esta última constituye un proceso de segundo orden,
mientras que la primera lo representa de primer orden, Sin embargo, para poder
relacionar con el trabajo este calor transportado, es necesaria aún otra limitación.
En efecto, ya que también puede tener lugar un transporte de calor sin efecto
mecánico, cuando un cuerpo caliente y uno frío están inmediatamente en contacto y
el calor fluye del uno al otro por conducción, entonces, si se desea lograr el
máximo de trabajo para el pasaje de una determinada cantidad de calor entre dos
cuerpos de determinada temperatura t y r, debe conducirse el proceso de tal modo que,
como ha ocurrido en los casos anteriores, nunca se pongan en contacto dos cuerpos de
diferente temperatura.
Ahora bien, es este máximo del trabajo que se debe comparar con el
pasaje del calor, y se encuentra que, en realidad, tenemos motivos para admitir, con
Carnot, que sólo depende de la cantidad de calor transportado y de las temperaturas t
y r de los cuerpos A y B, pero no de la
naturaleza del cuerpo intermediario. Este máximo tiene, en efecto, la propiedad de
que por el consumo del mismo también se puede transportar de nuevo del cuerpo frío B
al cuerpo caliente A una cantidad de calor igual a la que tenía que
pasar de A a B para su producción. Nos convencemos de
ello fácilmente si para su producción efectuamos en sentido inverso todos los
procesos descritos anteriormente, de modo que, por ejemplo, en el primer caso el gas
se dilata sólo de modo que su temperatura desciende de t a r,
luego prosigue su dilatación en contacto con B, después es comprimido
solo, hasta que su temperatura es de nuevo t, y finalmente sufre la
última compresión en contacto con A. Entonces, en la compresión se
consume más trabajo que el producido en la dilatación, de modo que en total tiene
lugar una pérdida de trabajo que posee el mismo valor que la ganancia obtenida en el
proceso anterior. Además, al cuerpo B se le quita tanto calor como el
que antes se le comunicó, y al cuerpo A se le comunica tanto como el
que antes se le quitó, de donde se deduce que no sólo se produce ahora la misma
cantidad de calor que antes se consumió, sino también que la misma cantidad que
antes fue llevada de A a B va ahora de B a A.
Si nos imaginamos ahora que existen dos sustancias de las cuales una
pueda dar mayor trabajo que la otra con un determinado pasaje de calor, o, lo que es
lo mismo, que para producir un determinado trabajo necesite transportar menos calor de
A a B que la otra, entonces podríamos utilizar
alternativamente a estas dos sustancias de modo tal que con la primera se produzca
trabajo por el proceso antedicho, y con la última se realice el proceso inverso
consumiendo el mismo trabajo. Entonces, ambos cuerpos estarían de nuevo, al final, en
su estado primitivo; además, el trabajo producido y el consumido se habrán anulado
exactamente de modo que también, de acuerdo con el principio anterior, la cantidad de
calor no pudo haber aumentado o disminuido. Sólo respecto a la distribución del
calor habría ocurrido una diferencia, en el sentido de que se habría transportado
más calor de B hacia A que de A hacia B,
y de este modo habría tenido lugar, en total, un transporte de B hacia A.
Por repetición alternada de ambos procesos se podría entonces, sin ningún gasto de
fuerza, o alguna otra transformación, llevar tanto calor como se quiera de un cuerpo
frío a otro caliente, lo que contradice el comportamiento ordinario del calor, puesto
que en todas partes muestra la tendencia a igualar las diferencias de temperatura, y a
pasar por lo tanto de los cuerpos calientes a los fríos.
De manera que parece teóricamente lícito mantener la primera
parte, y en realidad la fundamental, de la hipótesis de Carnot, y emplearla como
segundo principio junto con el anteriormente establecido; la exactitud de este
procedimiento, como enseguida veremos, ya ha sido también confirmada varias veces por
los resultados.
Según esta hipótesis, podemos caracterizar como función de t
y r al trabajo máximo que puede ser producido por el transporte de una
cantidad de calor desde el cuerpo A con temperatura t
hasta el cuerpo B con temperatura r. Esta función tiene
que ser naturalmente, con respecto a su valor, tanto más pequeña cuanto menos es la
diferencia t-r, y cuando ésta se hace infinitamente pequeña (=dt),
debe transformarse, en el producto de dt; por una función de t
solamente. Para el último caso, que es el que por ahora nos interesa, se puede, pues
representar el trabajo en la forma 1/Cdt, donde C significa una función
de t solamente.
Fragmento de Ueber die bewegendre Kraft de Wärme (1850).
Trad. de D. Papp (Buenos Aires, 1945).
Datos biográficos por M. en C. Arturo Noyola Isgleas
Del libro Panorama histórico de la ciencia moderna de
P. Lain Entralgo y José Ma. López Piñero.
![]()