EXPERIMENTO DE BOYLE

Robert Boyle (1627-1691)

Robert Boyle nació en Irlanda el 25 de enero de 1627. Hombre considerablemente rico, consagró su vida a la ciencia y a la religión. Sus conocimientos científicos fueron considerables y no realizó ningún descubrimiento de gran importancia conceptual, ni llevó su trabajo más allá de sus estados preliminares. Tuvo muy alta reputación por el número de contribuciones.

A la edad de ocho años fue a residir a Eton, donde demostró aptitud para el estudio y una gran disciplina.

De 1641 a 1642 vivió en Florencia; ahí conoció a Galileo, siendo el primero en estudiar los trabajos de éste. A la edad de 17 años, hecho ya un científico práctico y riguroso, regresó a Inglaterra. Fue miembro del Philosophical College, más tarde incorporado a la Royal Society.

Desde muy pequeño tuvo gran interés por la química, rechazó la alquimia, contribuyó a establecer la química como ciencia pura. En 1661 publicó un libro escrito en forma de diálogo intitulado: The Sceptical Chymist or Chymico Physical Doubts and Paradoxes, en el cual definió un elemento químico como una substancia simple, pura, la cual no podía dividirse en otras más simples por ninguna acción física o química. Se fundamentó en gran parte, en la hipótesis atómica de Demócrito. Hizo distinción entre mezclas y compuestos, preparó fósforo y desarrolló un método de análisis de varias sustancias. Desafortunadamente sus ideas químicas tuvieron poco efecto inmediato, hasta que Antoine Lavoisier (1843-1794) las revivió.

En 1654 Boyle se estableció en Oxford donde montó un laboratorio privado (un asistente fue Robert Hooke). Tres años después, habiendo aprendido de Otto von Guericke’s (1602-1686) la invención de la máquina de vapor, se propuso construir una, por lo que empezó sus investigaciones sobre las propiedades del aire. Demostró sus propiedades elásticas, que tenía peso, estudió el papel de la respiración y la combustión en la transmisión del sonido. Sus primeros resultados fueron publicados en Oxford en 1660 bajo el título de New Experiments Physico-Mechanical Touching the Spring of the Air and its Effects (Nuevos Experimentos físicos mecánicos referentes a la elasticidad del aire y sus efectos). La segunda edición en 1662 contenía su demostración experimental de la relación recíproca entre volumen y presión de un gas (aire), comúnmente conocida como Ley de Boyle. Mientras que la aproximación de estas medidas dejó mucho que desear, fueron lo suficientemente convincentes para ser aceptadas. Boyle no atribuyó mucha importancia a su descubrimiento cinco años más tarde Edmé Mariotte descubrió la misma relación independientemente.

Boyle se cambió a Londres en 1668, donde residía la Royal Society de la cual fue miembro fundador. Presentó sus resultados ante sus compañeros, entre los cuales se encontraba Newton, fue electo presidente de la Royal Society en 1680, él declinó el honor porque no podía suscribir el juramento, pero contribuyó grandemente al crecimiento de la sociedad.

Para hacer evidente que la elasticidad del aire es capaz de hacer mucho más de lo que le atribuimos, tratamos en los siguientes experimentos sobre de la razón de la elasticidad y volumen del aire.

MEDIDA DE LA CONDENSACION DEL AIRE

Teniendo mercurio puro en un tubo de vidrio en forma de J cerrado en el extremo más corto, colocamos a cada lado del tubo una tira de papel dividida en pulgadas, y cada una de éstas en ocho partes; y vaciando dentro del tubo mercurio, por la parte larga, observamos que el aire contenido en el tubo corto, el cual estaba herméticamente cerrado en la parte más alta de éste, era condensado por 29 pulgadas de mercurio, a la mitad del espacio que ocupaba antes, de donde se muestra, que si fue capaz de comprimirse a un estado tal, por virtud de su elasticidad, al resistir un cilindro de mercurio de 29 pulgadas, además del cilindro atmosférico obligatorio sobre él, se deduce que la compresión del aire abierto, a la mitad cuando más, debe tener la mitad del peso de la atmósfera que está sobre ella en el estado comprimido (el doble de la presión decrece a la mitad del volumen).

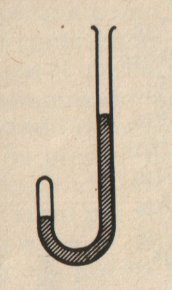
FIGURA 1

Para ser más exactos, consideremos el tubo representado por la figura 1, colocando en el brazo más corto un papel, dividido en doce pulgadas y cada una de éstas en cuartos, que dividimos en pulgadas y éstas a su vez en cuartos. Estando así marcado el tubo, el extremo más bajo fue colocado en una caja de madera, de modo que el mercurio podía corre en ella si la pipa sufría una rotura. Uno estuvo asignado a observar cuando el mercurio subía en el tubo pequeño a cada una de las divisiones mencionadas y llevaba notas, además veía cuál era la altura en el tubo largo al mismo tiempo; por lo que se efectuaron varias observaciones, las cuales están contenidas en la siguiente tabla: (Boyle supone que el interior del tubo era suficientemente uniforme, así que las alturas de las de las columnas de mercurio son medidas aproximadas de los volúmenes).

Pero en este experimento de prueba, cualquier derrame del mercurio debe hacerse por grados (una nota de precaución para futuros experimentadores, el mercurio debe verterse poco a poco), y de acuerdo con las indicaciones del que lleva nota de la ascensión del mercurio abajo, para lo cual es vertido con precaución, ya que pude pasar sobre las marcas colocadas en los tubos, antes de poder hacer la observación.

TABLA DE CONDENSACION DEL AIRE
A	A	B	C	D	E
48	12	00	Sumado 29 1/8	29 2/16	29 2/16
46	11 ½	01 7/16		30 9/16	30 6/16
44	11	02 13/16		31 15/16	31 12/16
42	10 ½	04 6/16		33 8/16	33 1/7
40	10 ½	06 3/16		35 5/16	35
38	10	07 14/16		37	36 15/19
36	9 ½	10 2/16		39 5/16	38 7/8
34	8 ½	12 8/16		41 10/16	41 2/17
32	8	15 1/16		44 3/16	43 11/16
30	7 ½	17 15/16		47 1/16	46 3/5
28	7	21 3/16		50 5/16	50
26	6 ½	25 3/16		54 5/16	53 10/3
24	6 ½	29 4/16		58 13/16	58 2/8
23	5 ¾	32 3/16		61 5/16	60 18/23
22	5 ½	34 15/16		64 1/16	63 6/11
21	5 ¼	37 15/16		67 1/16	66 4/7
20	5	41 3/16		70 11/16	70
19	4 ¾	45		74 2/16	73 11/19
18	4 ½	48 12/16		77 14/16	77 2/3
17	4 ¼	53 11/16		82 12/16	82 4/27
16	4	58 2/16		87 14/16	87 3/8
15	3 ¾	63 15/16		93 1/16	93 1/5
14	3 ½	71 15/16		100 7/16	99 6/7
13	3 ½	78 15/16		107 13/16	107 7/13
12	3	88 7/16		117 9/16	116 4/8

AA. El número de espacios iguales en el brazo más corto que contenía la misma cantidad de aire diversamente extendida.

B. La altura del cilindro de mercurio en el brazo más largo que comprimía el aire en esas dimensiones.

C. La altura del cilindro de mercurio, que contrabalanceaba la presión de la atmósfera.

D. El agregado de las dos últimas columnas B y C, presentando la presión mantenida por el aire incluido.

E. Lo que la presión podía hacer de acuerdo a la hipótesis, que supone a la expansión y a la presión en proporción recíproca. (Esta columna supone la relación bien conocida: PV=constante).

(La columna D indica que otros efectos como la temperatura no fueron importantes en estas medidas).

Teniendo por peso un cilindro de mercurio, se comprime el aire hasta un cuarto del espacio poseído anteriormente, observamos y pensamos que no puede condensarse más por frío, la flama de una vela cerca nos hace pensar que en un grado mayor de calor puede expanderse (de lo cual parece que la temperatura es llevada como constante), pero temiendo la ruptura del tubo, no osamos ponerlo a prueba.

Del experimento parece que como el aire es más o menos compresible, es capaz de contrabalancear un cilindro pesado o ligero de mercurio. Y que el mercurio estaba soportado por la elasticidad del aire condensado pareciendo succionar el aire de afuera del tubo cuando el mercurio tenía 100 pulgadas de altura en la pipa; por la presión de la columna obligatoria de la atmósfera, siendo removida por ese medio, el mercurio fue levantado en el tubo largo por la expansión del aire en el brazo corto del tubo, y no por cualquier funículo ya que como el objeto confiesa no puede levantarse más que un cilindro de treinta pulgadas (Franciscus Linus, apoyador de las doctrinas Aristotélicas había sugerido que el vacío de Torriceli contenido en una membrana dilatada invisible, llamada funículo, puede ‘tirar’ de una columna de mercurio a una altura máxima de cerca de treinta pulgadas, F. Linus es el objetor al que se refiere Boyle).

LA RARIFICACION DEL AIRE CONSIDERADO

Pero, junto con lo que se ha dicho aquí, no sólo puede ilustrarse un poco de nuestra doctrina sobre la elasticidad del aire sino observar cuánto se debilita la misma como efecto de la variación y rarificación de la expansión.

A continuación se da una tabla de la rarificación del aire

A	B	C	D	E
1	0	Resaltado a 29 3/4	29 3/4	29 3/4
1 ½	10 5/8		19 1/8	19 5/6
2	15 3/8		14 3/8	14 7/8
3	20 2/8		19 4/8	9 15/12
4	22 5/8		7 1/8	7 7/16
5	24 1/8		5 5/8	5 19/25
6	24 7/8		4 7/8	4 23/24
7	25 4/8		4 2/8	4 1/4
8	26		3 6/8	3 23/32
9	26 3/8		3 3/8	3 11/16
10	26 6/8		3	2 39/40
12	27 1/8		2 5/8	2 23/48
14	27 4/8		2 2/8	2 1/8
16	27 6/8		2	1 55/64
18	27 7/8		1 7/8	1 47/72
20	28		1 6/8	1 9/80
24	28 2/8		1 4/8	1 23/96

A. El número de espacios iguales en el tope del tubo, el cual contiene las mismas partes de aire.

B. La altura del cilindro mercurial, que junto con la elasticidad del aire incluido contrabalancea la presión de la atmósfera.

C. La presión atmosférica.

D. El complemento de B a C, mostrando la presión sostenida por el aire incluido.

E. La presión de acuerdo a la hipótesis

En este experimento puede notarse, primero, que podemos usar un tubo de vidrio de aproximadamente seis pies de longitud, cerrado en un extremo.

En segundo lugar, tenemos en consideración una pipa de vidrio, de diámetro aproximadamente igual a la de una pluma de cisne (cerca de ¼ de pulgada), el cual fue marcado con un papel introducido en él, dividido en pulgadas y medio cuartos, el cual fue sumergido en otro cilindro de mercurio abierto en ambos extremos, de modo que el mercurio puede levantarlo para llevar el otro extremo. Y con una pulgada sobre el mercurio, el orificio fue cerrado arriba; así que una pulgada de aire estaba contenida en el tubo, la cual, levantando el tubo, fue gradualmente expandida a varias pulgadas. Notando en un tiempo medio en varios pasos, cuánto mercurio estaba en el tubo pequeño por el aire expandido, permitiendo elevarse sobre la superficie del mercurio en el otro tubo: por lo cual el método de las observaciones que fueron hechas al principio. Al invertir el tubo largo, encontramos, considerando el experimento de Torricelli, que el aire sostenido por el mercurio era de 29 ¾ de pulgadas, observamos haciendo las medidas anteriores que la diferencia entre la cantidad la cual contesta nuestra hipótesis y la otra, se debe probablemente a un nuevo acceso de aire a la pulgada considerada, y realmente, cuando las observaciones fueron completadas, al remover el tubo encontramos que ha ganado sobre la mitad un octavo, lo cual juzgamos que puede deberse a alguna burbujas alojadas en los poros del mercurio. Del experimento parece que la pulgada de aire cuando expande al doble sus dimensiones, fue capaz, con un cilindro de mercurio de quince pulgadas de contrabalancear la atmósfera, la cual puede levantar el mercurio ocho y veinte pulgadas cuando la elasticidad del aire se halla perdido por una expansión (mientras que el doble del volumen del aire requiere unas quince pulgadas adicionales de mercurio para soportar la atmósfera, se sigue que la presión está siendo dividida en dos partes iguales aproximadamente). Así que la atmósfera aquí abajo puede consecuentemente estar comprimida igual que si veintiocho pulgadas de mercurio estuvieran sobre ella.

Del libro: Great Experiments in Physics (editado por: Morris H. Samos; traducido por Ma. Cristina Peña de Noyola, y revisado por M. en C. Arturo Noyola Isgleas).